Description
Volterra series based power amplifier model
The downloadable file contains the Matlab code that implements the Volterra series based power amplifier model when the input signal is OFDM with 256 subcarriers conveying complex data QAM signals.
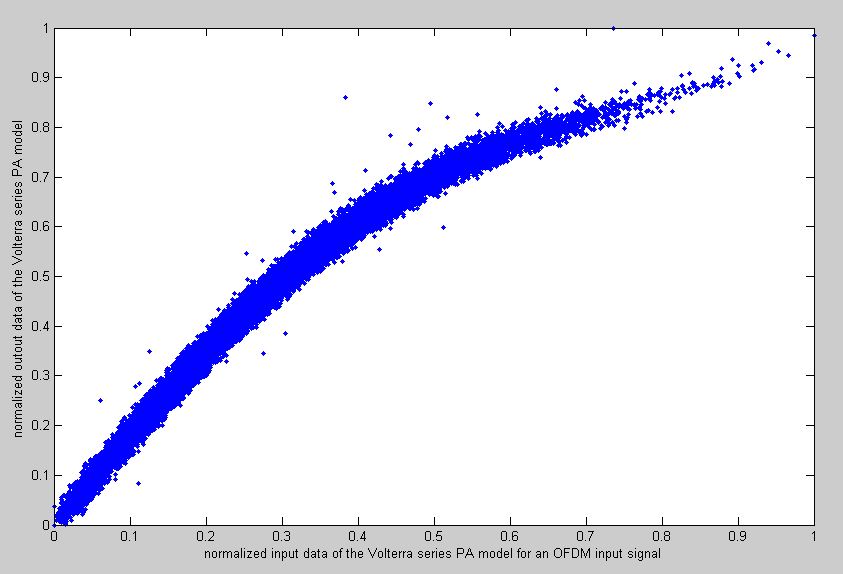
After running the code in Matlab, the following figure that shows the relationship between the input and output data of a Volterra series based power amplifier will be plotted. The model can be used to test, investigate, and quantify the performance and robustness of any transmission method or technique or scheme against the impairments of a practical power amplifier with memory effect. Most simulations nowadays are just focused on measuring the performance of communication systems over different types of wireless channels, but largely ignoring the effect of the memory effect and impairments caused when a realistic power amplifier is applied. This Matlab code will give you the opportunity to do that.
Introduction: Power amplifier are nonlinear devices responsible for compensating for the signal power loss between a transmitter and receiver. The input power levels to the power amplifiers can be increased to compensate for the power loss during transmission. At low input power regime, an ideal power amplifier provides constant gain to the output signal.
However, in the high input power regime, nonlinear effects of the power amplifier come to play, the power of the output signal shows diminished gain (compressed) and starts to saturate.
1-dB compression point is the most important measure of quantifying the beginning of non-linearity of the power amplifier (shown in the following figure). It is the point where the RF output power level decreases 1 dB from the constant value. Therefore, 1-dB compression point is a measure of the beginning of distortion, where a perfect sine wave fed at the input of the power amplifier do not maintain the perfect shape at the output of the power amplifier.

1-dB compression point
Memoryless models: Taylor series
Memoryless models place emphasis on the power amplifier with memoryless nonlinearity, which means that the current output is determined solely by the current input via a nonlinear method. A nonlinear memoryless system can be modeled using Taylor series. For example, a discrete time system with input x[n] and output y[n], the nonlinearity is incorporated using nonlinear terms with corresponding coefficients/weights (ɑi) for each term.
Memory models : Volterra series
The bandwidth of the signals, such as in 3GPP LTE and 3GPP 5G NR, gets wider. When the wideband signals are input to high power amplifiers (such as in base stations), the power amplifiers start to exhibit memory effects. As a consequence, the power amplifier’s current output is affected not only by the current input, but also by previous input values. Volterra series and its derivatives are commonly used to model power amplifiers with memory.
Volterra series is an useful tool for modeling nonlinear time invariant systems in general, and they are commonly used to model RF power amplifiers with memory effects. The Volterra series is a polynomial based mathematical model that captures the nonlinear terms and memory effects present in these devices.
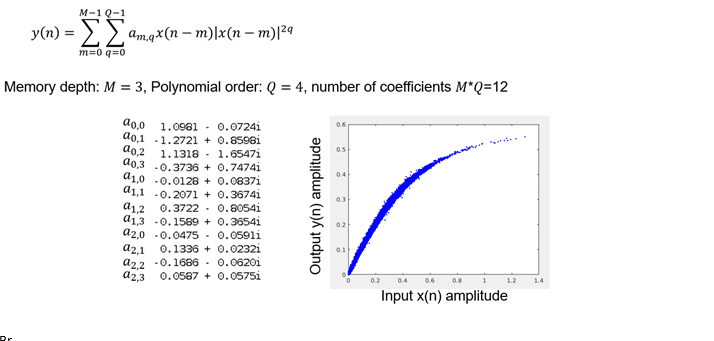
For a discrete time system with input x[n] and output y[n], the Volterra series with nonlinearity order K and memory depth Q is given by
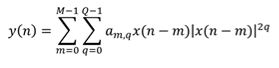
It can be understood that it models any system by using the system’s impulse responses. Because of the high complexity and high resource requirements, Volterra series cannot be used in practical applications.
For practical applications, Volterra series has to be truncated in such a way that it has the least impact on the models performance. This can be accomplished by omitting some of the terms in above equation for each application. Special versions of Volterra series allow for use in power amplifier behavioral modeling. Memory polynomial model is one of the derivative of Volterra series that is easier to implement.