About Course
The goals for this Fourier Analysis course are to gain a facility with using the Fourier transform, both specific techniques and general principles, and learning to recognize when, why, and how it is used. Together with a great variety, the subject also has a great coherence, and the hope is students come to appreciate both.
Fourier Analysis Topics include: The Fourier transform as a tool for solving physical problems. Fourier series, the Fourier transform of continuous and discrete signals and their properties. The Dirac delta, distributions, and generalized transforms. Convolutions and correlations and applications; probability distributions, sampling theory, filters, and analysis of linear systems. The discrete Fourier transform and the FFT algorithm. Multidimensional Fourier transforms and uses in imaging. Further applications to optics. Emphasis is on relating the theoretical principles to solving practical engineering and science problems.
Course Content
Fourier Analysis
-
Fourier Analysis: Overview
00:00 -
Computing Derivatives with FFT [Python]
00:00 -
Solving PDEs with the FFT [Matlab]
00:00 -
Solving PDEs with the FFT [Python]
00:00 -
Solving PDEs with the FFT, Part 2 [Matlab]
00:00 -
Solving PDEs with the FFT, Part 2 [Python]
00:00 -
The Spectrogram and the Gabor Transform
00:00 -
Spectrogram Examples [Matlab]
00:00 -
Spectrogram Examples [Python]
00:00 -
Uncertainty Principles and the Fourier Transform
00:00 -
Wavelets and Multiresolution Analysis
00:00 -
Image Compression and the FFT
00:00 -
Image Compression with Wavelets (Examples in Python)
00:00 -
Image Compression with the FFT (Examples in Matlab)
00:00 -
Image Compression and Wavelets (Examples in Matlab)
00:00 -
Image Compression and the FFT (Examples in Python)
00:00 -
The Laplace Transform: A Generalized Fourier Transform
00:00 -
Laplace Transforms and Differential Equations
00:00 -
Computing Derivatives with FFT [Matlab]
00:00 -
Denoising Data with FFT [Python]
00:00 -
Denoising Data with FFT [Matlab]
00:00 -
Fourier Series: Part 1
00:00 -
Fourier Series: Part 2
00:00 -
Inner Products in Hilbert Space
00:00 -
Complex Fourier Series
00:00 -
Fourier Series [Matlab]
00:00 -
Fourier Series [Python]
00:00 -
Fourier Series and Gibbs Phenomena [Matlab]
00:00 -
Fourier Series and Gibbs Phenomena [Python]
00:00 -
The Fourier Transform
00:00 -
The Fourier Transform and Derivatives
00:00 -
The Fourier Transform and Convolution Integrals
00:00 -
Parseval’s Theorem
00:00 -
Solving the Heat Equation with the Fourier Transform
00:00 -
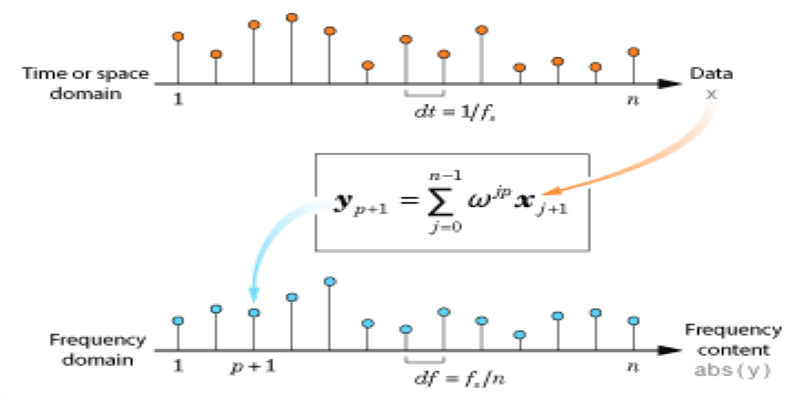
The Discrete Fourier Transform (DFT)
00:00 -
Computing the DFT Matrix
00:00 -
The Fast Fourier Transform (FFT)
00:00 -
The Fast Fourier Transform Algorithm
00:00 -
Laplace Transform Examples
00:00
Student Ratings & Reviews

No Review Yet
